|
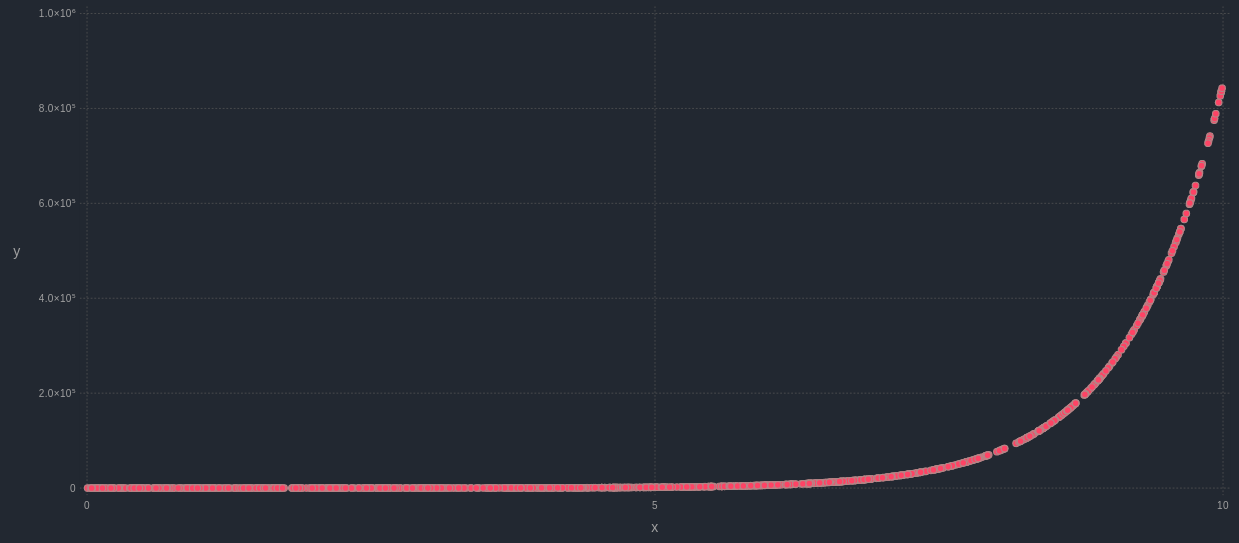
Before someone says “yes, of course; you just need to apply a non-linear transformation to one of the variables!”, let me rephrase: can we measure a non-linear relationship between two variables, without any transformations whatsoever? In other words, is there a heuristic metric that can facilitate the task of establishing whether two variables are linked in some fashion, without any data engineering from our part? The answer is “yes, of course” again. However, the relationship has to be monotonous for this to work. In other words, there needs to be a 1-1 relationship between the values of the two variables. Otherwise, it may not appear as strong, due to the nature of non-linearity. So, if we have two variables x and y, and y is something like x^10 + exp(x), that’s a relationship that is clearly non-linear, but also monotonous. Also, the Pearson correlation of the two variables in this case is not particularly strong (for the variables tested, it was about 0.67). If it were measured by a different correlation metric, however, like a custom-built one I’ve recently developed, the relationship would be somewhat stronger (for these variables, it would be around 0.75) while Kendall's ranked correlation coefficient would produce a great result too (1.00 for these variables). In a different scenario, where z = 1 / x, for example, the results of the correlation metrics differ more. Pearson’s correlation in this case would be something like -0.16, while the custom-made metric would yield something around -0.69. Also, Kendall’s coefficient would be -1.00. Although the effect is not always pronounced, in cases like this one, a different metric can make the difference between a strong correlation and a not-so-strong one, affecting our decisions about the variables. Bottom line, even if the Pearson correlation coefficient is the most popular method for measuring the relationship between two variables, it’s not the best choice when it comes to non-linear relationships. That’s why different metrics need to be used for evaluating the relationship between two variables, particularly if it’s a non-linear one.
0 Comments
Your comment will be posted after it is approved.
Leave a Reply. |
Zacharias Voulgaris, PhDPassionate data scientist with a foxy approach to technology, particularly related to A.I. Archives
April 2024
Categories
All
|
 RSS Feed
RSS Feed