Introduction
I've written about Nim in the past, but it's been a while. So, I decided to do a deep dive on it this time as the language seems to have evolved a lot since then, plus I had promised that I'd keep an eye on it. So, let's look at this language anew and explore how it's faring these days.

Why Nim and why it's worth learning about it
Nim has been around for almost a decade and a half now but it remains in relative obscurity. So, why should you learn about it nevertheless, especially when there are other, more established languages out there? Well, Nim is super fast (it compiles to C, so you can expect similar performance), it's very intuitive in its syntax (especially if you are coming from a Python background), and it's versatile. It also has a committed team without a big company behind it, making it the de facto underdog of programming languages.

Despite its hardships, it has managed to get a production-ready version out and find some niche use cases to make it stand out from the crowd. Its documentation is pretty good (much better than many other languages' docs) while its official website even has some comprehensive tutorials for learning Nim. It has a variety of packages and it's constantly growing in its codebase, making it a very promising language still, against all odds.

Nim from a Pythonista's perspective
Although Python is hardly a "real" programming language and shouldn't be compared to languages like Nim that do some real heavy lifting, these days it's in vogue. It's a fairly decent scripting language ideal for someone who's never learned the ins and outs of computers and how they work. Perhaps that's why it's so popular today. What Python does well is its syntax and the simplicity of its code. Some call it pseudocode that runs and they aren't wrong. Once you get accustomed to its idiosyncrasies, Python is fairly straightforward to work with while its code is very similar to the pseudocode version of an algorithm. Nim adopts this attribute of Python, making its code very intuitive and comprehensible, even to newcomers to the language.

So, for a Pythonista, Nim will seem strangely familiar and should be easy to understand from the very beginning. This was probably a design decision, to make the barrier of entry to the language as low as possible. It's noteworthy that the language under the hood is quite different though as the memory management, the indexing, and the whole approach to variable-setting are closer to that of low-level languages. So, it may still require some effort to learn Nim properly, even if you have mastered Python.

Nim from a C programmer's perspective
As Nim is somewhat closer to C than any other language, it also is easy for a C language user. After all, the Nim compiler gives you the option to see the C code of each Nim program you create. If you are used to the curly brackets that C features in its programs, Nim gives you the option of writing your scripts similarly, using parentheses instead. This way, the barrier to entry to this language shouldn't be too high in this case either. The fact that it uses 0-point indexing like C and similar data structures makes Nim familiar even to C programmers.

Nim's compiler is much better, however than that of C and any other low-level language. It can pinpoint issues so that you don't have to worry about the executables once they are created. It can also provide you with some useful feedback to make troubleshooting easier. Additionally, memory management is better than C and overall it's easier to work with Nim as it's more high-level as a language.

Nim from a data professional's perspective
From a data professional's perspective, Nim is getting there. Even if its base package doesn't support any complex data structures that lend themselves to real-world data (like Julia does, for example), it has a plethora of external packages that do the trick. So, the language seems to be data-ready right now, even if it's hard to see it competing with Python or Julia for data-related work, right now. After all, beyond the coding capabilities of a language, other factors come into play, such as the language's integration with Jupyter notebooks. Kotlin integrates smoothly (even if it is a compiled language like Nim), but Nim's integration is iffy. Some commands like the one requiring input from the user don't seem to work at all, plus the Jupyter integration module is fairly new, compared to that of other programming languages.

Additionally, Nim doesn't have a large data science community, making it a bit more challenging for a Nim learner from the data science field to feel at home. Although this may change in the future, it seems that only the most committed data scientists can find Nim a valuable tool for analytics-related work. Nevertheless, Nim lends itself to data engineering work as it has various database and data file packages, while its speed makes it ideal for this sort of task.

Nim's role in Cryptography and Cybersecurity
What about cryptography though and cybersecurity in general? Well, in this niche Nim seems to thrive. It has mature libraries for randomness and hashes, while it's fairly easy to code something related to this field from scratch. The fact that it's very fast makes it ideal for this kind of application. Also, Nim's ability to create small executables gives it more flexibility and enables it to emulate "red team" scenarios, so that the "blue team" can better prepare for cyberattacks.

It's a shame that the cybersecurity and cryptography communities aren't as open-minded about alternative programming languages to give Nim a shot. This language has a lot to offer here and it wouldn't be surprising if in the future more applications in these fields find themselves coded in Nim. This is likely going to happen through hobbyists and independent researchers with a knack for programming though.

Nim prospects
Beyond all these facets of Nim, the language seems to have a promising future right now. There are several projects in the works, it has a UI framework, and the number of content creators writing about Nim has increased. More people are becoming aware of the value-add the language offers, while the world's obsession with Python is being challenged as more easy-to-code-in languages enter the coding sphere.

Although it's unlikely it will ever be as popular as the languages that have come to dominate, it's bound to continue and become better as its community grows. Nowadays there are even conferences on Nim and the language seems to become easier to adopt and acknowledge, at least for certain use cases that systems computing. The big milestone, however, would be if Nim enters the world of code learning platforms like CodeAbbey, where people can solve interesting challenges using the language and refine their skills in the process. The fact that it's already on Exercism and Rosetta Code, however, is a step in the right direction.

Final thoughts about Nim
So, there you have it. Nim is a powerful programming language with quite a few things to offer, as it's heading toward version 2.0. Whether it will get a large enough following is up to you as most people tend to shy away from language that doesn't have the backing of a large company or academic institution. Also, it seems that lately there are lots of languages out there, so deciding to commit to this one is even more challenging. Yet, those who have delved into Nim can see its merit and are likely to continue with it. Even if it doesn't make it big like the languages it borrows from, it's bound to stick around and thrive in its niches.
​

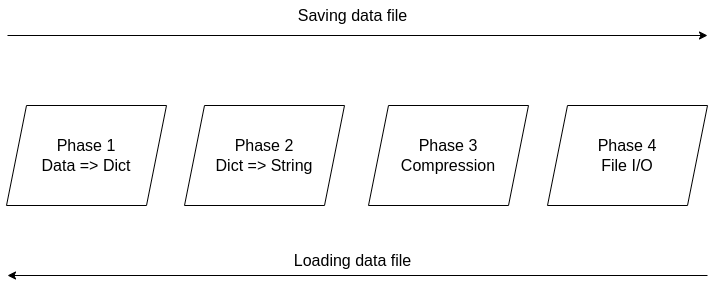
It's been over two years since the Compressed Data Format (CDF) made its debut, making storing data files in Julia a breeze. Not only does it handle various types of data easily, but it also allows for comments and any other stuff you'd like to include in your data file before sharing it with other Julia users. The native data file formats the language has been okay, but when it comes to larger datasets, they fall short. Also, conventional data file formats like CSV and JSON, although mature and easy to use, tend to be bulky as the number of data points/variables grows. CDF remedies all that by employing a powerful compression algorithm on the data at hand. 

The CDF script consists of a series of functions while it leverages another script for handling binary files. Because if you want to do anything meaningful with files, you need to go down to the 1s and 0s level. The conventional IO handling Julia offers is fine, but it's limited to text files mainly. However, the language has binary file capabilities, which are leveraged and simplified in the binfiles.jl script that CDF relies on for its IO operations. That script has just two functions, one for reading binary files and one for writing them. Naturally, everything on that level is expressed in Int8 vectors, as a data stream related to a binary file is a series of bytes, often in the form of an 8-bit number (ranging between -128 and 127, inclusive. So, if you wish to delve into this sort of file operation, make sure you familiarize yourself with this data structure. 

Fortunately, the CDF script is more high-level than the binfiles.jl one. Still, it needs to deal with binary files at one point, so it has to translate the data streams it handles into Int8 vectors. To make the most of the bandwidth your machine has, it breaks down the whole process into these distinct phases, which you can view in Fig. 1:
1. Turning the data into a Dict object if it's not in that form already.
2. Turning the dictionary into a text stream (string variable).
3. Compressing the text stream.
​4. Passing the compressed data into the binary files function to read/write the corresponding files.

​
The handling of the binary files takes place using the binfiles.jl script, as mentioned previously, so we won't cover it in depth in this article. For the remaining phases, let's start from the easy part: compression (phase 3). Here the CodecZlib package is used, which contains a bunch of compression algorithms. The CDF script leverages the Deflate algorithm due to its speed and efficiency. Naturally, as everything is already in the form of a string variable by that stage utilizing the compression algorithm is pretty straightforward.

Now the problem becomes turning everything into a string (phase 2). Although this seems straightforward, doing that all while ensuring that the whole process is easily reversible can be challenging. Fortunately, if everything is already in dictionary form, it's not that hard. After all, a dictionary comprises various keys which correspond to certain values, all of which can be retrieved through the keys() and values() functions of the dictionary class. So, handling a dictionary isn't that hard, and it can be done methodically. Of course, dumping the dictionary's contents into a string file isn't a great idea since the various key-value pairs need to be separated. One way to do this, which is also the way CDF is written, involves putting all the keys together in the beginning and then all the values corresponding to these keys. Each key is separated from the next using a space (the keys correspond to variable names, so they tend to be void of spaces). From that point on, for all pieces of data that need to be connected in that output string, a special character is used, one which doesn't come into play in data files. This way, it's easy to split the string between the keys and the values, using that special character as a separator. The same goes for all the different values that are added to the string. Since they might contain spaces in them, we use the special character to separate each from the next. Following that, we also store the types of these values so that we can reconstruct the original contents of the dictionary. The types are contained in a separate array and are separated by spaces. To make this information more easily accessible, we position it at the end of the string, separated from the values part using the special character.

To create the dictionary (phase 1), we merely need to put the variable at hand into an empty dictionary, with the variable name as its key and its contents as its value (this is done automatically with the corresponding function of the CDF script). This process is a bit more cumbersome a process as it requires the user to input both the variable and its name, while it’s limited to a single variable (e.g., a matrix of a dataset). That’s why it’s generally better to have all the data available as a dictionary before using the CDF script. This way, if you need to add any comments to the data, you can do so by adding another key-value pair to the dictionary where the data lives.

The data types supported by CDF at this stage are String, Char, Real, Float64, Int64, and Array of numbers of bits. In future versions of CDF, it may also be able to handle more complex scenarios, such as DataFrames, nested arrays, arrays of strings, etc.

CDF can be useful for storing models too, with the (hyper)parameters being in a particular part of the dictionary, the operational conditions in another part and some metadata about the training data and the model's tested performance in another part. This way, by loading this CDF file, you can get all the relevant information about the model to use in your project.
​

Although I really enjoy Julia and other new programming languages, I also use Python, SQL, etc. for various projects. Beyond that, I tend to mentor students in these more conventional languages, as it's part of their curriculum. Learning these languages, however, often comes at a cost and if someone has already shelled thousands of dollars in a course, it's doubtful they would be willing to spend more to go deeper on these subjects.

Fortunately, AIgents has you covered. This Data Science and AI platform for practitioners and learners in these fields recently launched a learning branch on its website, featuring a selection of useful resources for learning these technologies (these live on various sites, which you can find on your own but AIgents saves you time by do this tedious task for you and curating them to some extent). The best part is that all of these resources are free while there is also a community this platform has, to facilitate further such initiatives. You can check it out here. Cheers!
​

Unfortunately, datasets aren't as easy to gauge as the butterflies in this picture. Yet, even if the simpler cases where we can make a descriptive plot to highlight the geometry involved, similarity is not a binary matter. Two datasets may be somewhat similar or dissimilar, without being identical or in stark contrast. So, how could we gauge similarity in an N-dimensional space?

The simplest thing to do is run a bunch of t-tests, one for each variable involved. This approach may be fine for someone new to the field (especially if the people managing this person's team aren't knowledgeable about these matters), but it won't work well. There are several underlying assumptions in this strategy that rob it of its validity and, possibly, its effectiveness.

The Index of Congruence is a simple heuristic based on the Index of Peculiarity, which in turn is congruent to the Index of Discernibility (though not focused on classification scenarios per se). The Index of Congruence does one simple thing: gauge the similarity of two matrices of real numbers on a scale of 0 to 1 with high values denoting strong similarity. It's not perfect but it does what it sets out to do, and does so swiftly. If one of the datasets is larger than a given threshold, some (random) sampling takes place in both datasets, preserving the original ratio in sizes, before the heuristic is applied. Also, normalization takes place in the back-end without worrying the user, since we have better things to do than worry about the scale of the variables at hand, right?

I could write about this heuristic for a while, but I'm sure you'd rather see it in action. So, I'm attaching a Jupyter notebook that you can check out on your own. No, I haven't switched to this kind of code notebook as I'm still in favor of Neptune notebooks, but when it comes to showcasing something, Jupyter notebooks remain the best option. Cheers!
​

Lately I published an episode of my podcast where I talk about compression and encryption as privacy tools (link). That’s all nice and dandy but how do we do any of that in practice? Well, most compression programs have an encryption option, which may be sufficient for low-confidentiality documents. But what about datasets that contain lots of PII? And if you are like me, you may use Julia for processing them, since it’s by far the most efficient programming language for the task, that’s also high-level.

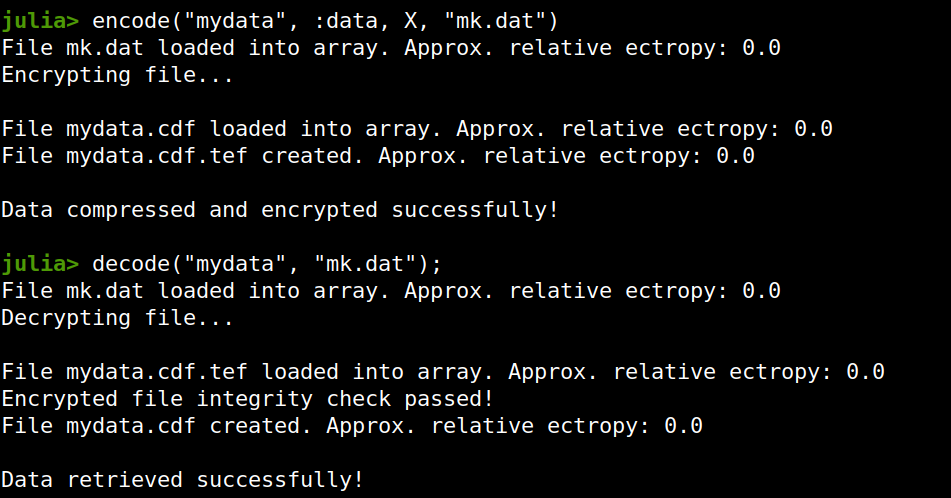
​Enter ComCrypt, a simple script that does high-quality compression and quantum-proof encryption all in one go. Namely, it makes use of the CDF script which I’ve talked about before (it’s been about two years since I created it) for compressing the data into an archive having the .cdf extension (which stands for compressed data format and it’s native to Julia). Then it applies ThunderStorm to it, using an external key file. If anything goes wrong throughout this process, ComCrypt alerts the user with some error message informing about the part that threw the error. Otherwise, it yields a message saying that the data has been compressed successfully. The reverse process shares the same philosophy. 

​Currently, ComCrypt at its first version so its scope is a bit limited (e.g., it handles only a single data object per file). However, there are ways to make it more usable and useful. In any case, it’s already a useful little tool for keeping your data safe when working in the Julia environment. Also, it’s very light on the dependencies (just one external library and a few Julia scripts). Cheers.

Overview
I've been working on this cipher for several years now, and although it's not the first one I've developed, it's the best one, so far. Not just in terms of security but also in speed and customization. I haven't touched the algorithm in a couple of years now, but I recently did some updates on its shell functions and its GUI for better usability. But I'm getting ahead of myself. Let's start with some basics first, in case you are not familiar with it.

What ThunderStorm Is
ThunderStorm is a semi-symmetric encryption system designed for codes impenetrable by  conventional cryptanalysis methods. Unlike other encryption methods, it doesn't rely on prime  numbers and factoring, while it employs true randomness in the keys it uses for additional security. It currently exists in two versions: one that's order-sensitive and one that's purely symmetric and  order-indifferent. The former makes for a stronger cipher, while the latter is lighter.  ThunderStorm is implemented entirely in Julia (recently tested in v.1.7.2 with no issues) and has minimal dependencies on any libraries.

How It Works
In a nutshell, ThunderStorm works as follows. It captures all the relevant information regarding the  size of the original file and its hash. It then encrypts it using the hash of the key. This is the header  of the encrypted archive. Then a random amount of noise is created and added to the original file.  After that, the data is encrypted and shuffled using the key, in a byte-wise fashion. The resulting  archive, which is somewhat larger than the original is outputted using a file extension that makes it  clear what it is. For the decryption process, the reverse is done. Note that if a single bit in the key  file is off, the decryption process won't work, or if it does, it will yield a completely different file  that would be unrecognizable. Also, if you were to take a random byte in the encrypted archive  there is no way of knowing if that byte is an encrypted part of the original file (it could be just  noise) or if it is which part of the file it comes from or what it is exactly. Also, only part of the key  is usually used for the encryption, while its parts are shuffled before being utilized in the encryption  process. I had published a video on ThunderStorm back in my Safari days, but it's no longer available since the contract with O'Reilly (which acquired Safari at one point) came to an end.

ThunderStorm Use Cases
The ThunderStorm system has several real-world use cases. Primarily, it is ideal for individual use,  particularly for static documents (e.g., a password archive, financial records, etc.). This includes  documents that are stored in the cloud or a web server. Additionally, ThunderStorm can be modified  to be used for exchanging sensitive documents, where increased cybersecurity is a requirement. For  all the use cases, large encryption keys are strongly recommended, something possible through an  auxiliary method of the ThunderStorm system. A large key can be manufactured in such a way that  it has zero ectropy (i.e., maximal entropy possible), making cryptanalysis extremely difficult if not  altogether impossible. The fact that keys can be reused in ThunderStorm with minimal risk is an  asset that can be harnessed for efficiency.

Latest Improvements
Since I'm a big fan of continuous improvement (Total Quality Management), I decided to make a GUI for ThunderStorm, even though I'm not a GUI kind of guy. Still, after having developed my BASH scripting skills enough, I was able to do that. So, recently I came up with a new script that leverages a few window screens to facilitate the use of this program. It still uses Julia on the back-end, but it can run directly from the shell (or the file manager, if you prefer). Below are some screenshots of the interactive aspects of that script. Note that some of the functionality of ThunderStorm was removed to make the whole program easier for the average user. For the more tech-savvy users, the functionality remains and can be accessed through the corresponding Julia scripts.
​

Parting Thoughts
Probably this is not the last update on ThunderStorm since it's been my pet project for a while now. Also, considering how feeble most ciphers are when it comes to the quantum threat, someday enough people may see value in a robust and unconventional cipher, to warrant further R&D on it. Until then, it will probably remain a niche thing, much like the language it was written in, as most high-level developers prefer to stick with the languages they know instead of going for a newer and objectively better language like Julia. Cheers!
​

Introduction
Code notebooks have become a necessity for anyone doing any serious work in this field. Although they don't have the same functionality as IDEs, they are instrumental, especially if you want to showcase your code. Also, it's something that has evolved quite a bit over the years. This notebook covered in this article is seemingly the latest development of this evolution, at least for the Julia programming language, in data science work.

Don’t You Mean Jupyter Notebooks?
I understand why someone would think that. After all, Jupyter notebooks are well-established, and I've often used them myself over the years. However, this code notebook I write about is an entirely different animal (you could say another world altogether!). Neptune notebooks have little to do with Jupyter ones, so if you go to them expecting them to be just like Jupyter but better, you'd be disappointed. However, if you see them for what they are, you may be in for a surprise.

A Voyage through the Solar System of Code Notebooks
Neptune notebooks are essentially Julia scripts rendered on a web browser. At the time of this writing, this browser is usually Chrome or some variant of it (e.g., Chromium) and Firefox.  However, The latter browser isn't ideal for particular tasks, such as printing (even if it's PDF printing).

A Neptune notebook can run on Julia, even if you don't have the Neptune.jl library installed. However, if you do, you can load the notebook on your browser and have Julia running in the background, just like in the Jupyter notebooks. However, unlike its more established brother, the Neptune notebook only supports Julia, particularly the later versions of the language. Also, the layout is quite different, and at first, it may seem off-putting if you are used to the elegance and refined interface of Jupyter notebooks.

Neptune notebooks are rudimentary, perhaps even minimalist, compared to Jupyter ones. However, because of this, they are far more stable and efficient. In fact, in the few months that I've been using Neptune notebooks, I've never had it crash on me, not once. Also, authentication errors are rare and only happen if you try to run a Neptune notebook on both Firefox and Chromium simultaneously. The notebook seems to lock onto the browser you start it in, usually the default browser. Wrinkles like this will hopefully be ironed out in future versions of the Neptune library. Despite them, however, these notebooks are quite slick and their support of markdown is a noteworthy alternative to the text cells of Jupyter notebooks. Perhaps overall, they are geared towards the more advanced users at the time of this writing. Hopefully, this is something that will change if more data scientists embrace this technology.

By the way, technically Neptune is a form of the Pluto.jl library, which enables Pluto notebooks. However, the latter, although quite interesting, aren't designed for data science work and I'd not recommend them. If, however, you are a Julia programmer who wants to use something different, Pluto is a good alternative. Just don't try to do a data science project on them before getting some insurance policy on your computer, since it's likely you are going to physically break it, out of frustration!

Final Thoughts
The development of code notebooks is fascinating, and Neptune seems to be a respectable addition to all this. As there aren't any decent tutorials at the moment that I can point you to, I suggest you play around with such a notebook yourself to see if it does it for you. If you want to see one such code notebook in action, you can check out my Anonymization and Pseudonymization course I've published relatively recently on WintellectNow. All the coding in it is on a Neptune notebook, which is the hands-on part of that mini-course. Cheers.

This topic may seem a bit strange, but I'm running out of ideas here! Still, it's interesting how often this topic comes about in mentoring sessions, especially when dealing with A/B testing. So, if you can't answer the question "when are two numbers equal enough?" in a simple sentence, perhaps you'll have something to learn from this article.

First of all, the rationale of all this. Sometimes, we need to make an executive decision about whether we should apply this or the other function on the data at hand. In A/B testing, this is usually something like “should we go for the equal variances or the unequal variances variant of the T-test?” Of course, when you have two samples, the chances of their variances being exactly equal is minuscule, so why did those old sages of Stats whom we revere so much decide to have two variants of the T-test, based on the equality of the variances involved? Well, there is a different formula used since if the variances are the same, things are much simpler with the underlying math. But then the question becomes "when are these two variances equal?" and keep in mind that we are talking Stats here, so the rigidity of Math as we know it doesn't apply. We are comfortable with approximations, otherwise, we'd have to abandon the whole idea of Statistics altogether!

In engineering, two numbers are equal when their difference is within a tolerance margin. We usually depict this tolerance by a threshold th expressed as a negative power of ten. So, often we have something like th = 10^(-3), which is a fancy way of saying th = 0.001. This kind of approximation, although very handy, may not apply to the problem at hand. Besides, few disciplines have the scientific reasoning and discipline that Engineering exhibits, and Stats is not one of them. Also, let's not forget that traditional Computer Science is akin to Engineering, so the approx() function found in many languages follows a similar motif, making it inapplicable to the problem mentioned previously.

In Physics, things are a bit different, which is why often we talk about orders of magnitude. So, it's often the case that if two quantities A and B are different by at least an order of magnitude, they are much different. This is another way of saying that one is at least ten times bigger than the other. This is something we can apply to our problem since it gives us a relative rule of thumb to work with. Of course, an order of magnitude is quite a bit when we talk about variances, but we can adapt this to something that makes more sense in Analytics work.

So, what about a fixed percentage, maybe one order of magnitude less than 1? This would translate into 10% (since 1 = 100%), something that's not too much but not negligible either. So, if v1 and v2 are the two variances at hand, we can say that if v1 <= (1+10%)v2 and v2 <= (1+10%)v1, we can presume v1 and v2 to be more or less equal. Additionally, this wouldn't work if one of them is 0, in which case the two variances would always be considered different from each other. Then again, this makes intuitive sense since we'd be dealing with a static variable and one that varies at least a bit. Also, as things are made simpler if we use as a reference point the smaller variance, we can just do a single comparison and be done with it. After all, if v2 is the smallest and v1 <= 1.1*v2, we can be sure that the reverse would also hold true.

In other words, we can use a script like the one attached to this article and not have to worry about this matter much (note that this script allows us to use a different threshold too, other than 0.1). Cheers!

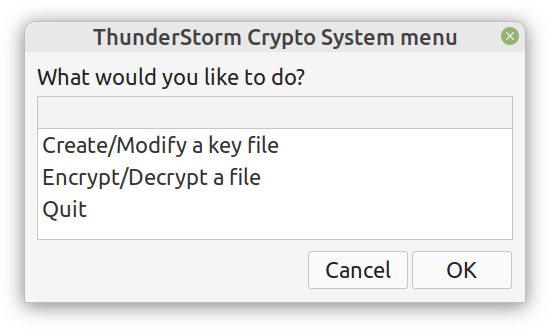
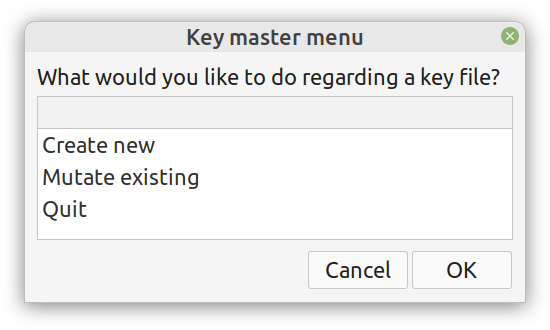
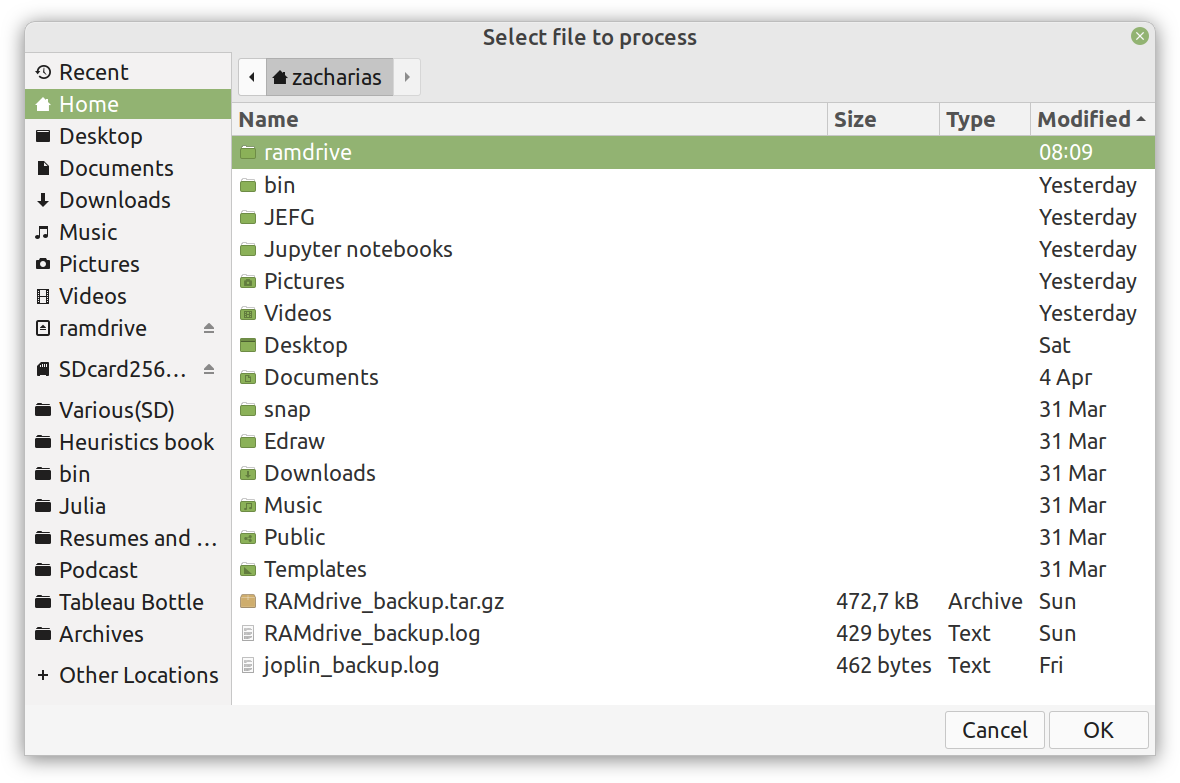
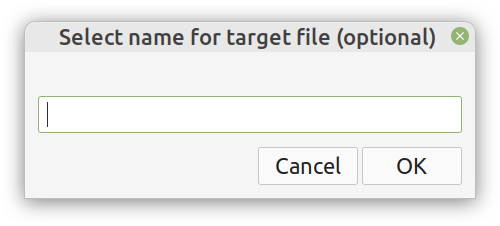
The latter has been something I've been looking into for a while now. However, my skill-set hasn't been accommodating for this until recently, when I started working with GUIs for shell scripting. So, if you have a Linux-based OS, you can now use a GUI for a couple of methods in the Thunderstorm system. Well, given I'll release the code for it someday.

Alright, enough with the drama. This blog isn't FB or some other overly sensational platform. However, if you've been following my work since the old days, you may be aware of the fact that I've developed a nifty cipher called Thunderstorm. But that's been around for years, right? Well, yes, but now it's becoming even more intriguing. Let's see how and why this may be relevant to someone in a data-related discipline like ours.

First of all, the code base of Thunderstorm has been refactored significantly since the last time I wrote about it. These days, it features ten script files, some of which are relevant in data science work, too (e.g., ectropy_lite.jl) or even simulation experiments (e.g., random.jl, the script, not the package!). One of the newest additions to this project is a simple key generation stream (keygen) based on a password. Although this is not true randomness, it's relatively robust in the sense that no repeating patterns have emerged in any of the experiments on the files it produced. Some of the key files were several MB in size. So, even though these keys are not as strong as something made using true randomness (a TRNG method), they are still random enough for cryptographic tasks.

What's super interesting (at least to me and maybe some open-minded cryptographers) is a new method I put together that allows you to refresh a given key file. Naturally, the latter would be something employing true randomness, but the particular function would work for any file. This script, which I imaginatively named keys.jl, is one I've developed a GUI for too.

Although I doubt I'll make Thunderstorm open-source in the foreseeable future (partly because most people are still not aware of its value-add in the quantum era we are in), I plan to keep working on it. Maybe even build more GUIs for the various methods it has. The bench-marking I did a couple of months back was very promising for all of its variants (yes, there are variants of the cipher method now), so that's nice.

In any case, it's good to protect your data files in whatever way you can. What better way than a cipher for doing this, especially if PII is involved? The need for protecting sensitive data increases further if you need to share it across insecure channels, like most web-based platforms. Also, even if something is encrypted, lots of metadata from it can spill over since the encrypted file's size is generally the same as that of the original file. Well, that's not the case with the original version of Thunderstorm, which tinkers with that aspect of the data too. So, even metadata mining isn't all that useful if a data file is encrypted with the Thunderstorm cipher.

I could write about this topic until the cows come home, so I’ll stop now. Stay tuned for more updates on this cryptographic system (aka cryptosystem) geared towards confidentiality. In the meantime, feel free to check out my Cybersecurity-related material on WintellectNow, for more background information on this subject. Cheers!

What Rust is
I may have mentioned Rust in the past, but now I’d like to talk more about it and its role in data science and A.I., as it has passed the test of time, in my view. After having delved into Rust programming a bit, enough to understand that it's much more challenging than I realized at first, I believe I can now write about it with confidence. Also, since it's not so new to me, I'm way past the infatuation stage that characterizes most people who have talked or written about it, usually shortly after they started exploring it.

So, Rust is a high-performance language, currently in version 1.51, and with a large enough community of users (and companies) to make a dent in the programming realm. There is even a Rust track in the Exercism platform, where there are dedicated mentors who can help you learn it through the carefully designed and curated programming drills on the Exercism website. What's more, there are a few interesting books on Rust, while there are also conferences and workshops for anyone serious about this language.

Rust’s key strengths
Rust isn't popular because of its particular name or its cool logo, though. Rust earned its popularity through the strengths it brings to the table and the value-adds that accompany its deployment. First of all, it's high-performance, meaning that you can use it instead of C, C++, or even Java. That's not an easy-to-accomplish thing, and few languages have accomplished that. Also, it offers this performance while maintaining a relatively high-level approach to programming, much like most modern languages that come about.

Additionally, Rust is reliable and as safe as it gets. Many consider it to be better in that respect than even C, which has a series of memory management issues resulting in risky code. So, if you want to build a program that just works and won't make you sleep with your phone on at night (in case you'll need to fix an issue of a script you've shipped), Rust is a good option.

Finally, Rust is geared towards productivity. It's not an academic language or something a bunch of hobbyists put together, far from that. Rust is built for devs and people who are dead serious about designing and deploying software. The language's well-written documentation adds to this. At the same time, its error messages, although frustrating at first, give you some actual insight as to what's wrong with your scripts (instead of some generic error message that's more of a puzzle than any real help for debugging your code).

Rust and Data Science
When it comes to data science work, particularly machine learning and AI-related tasks, Rust has the potential of being a great asset. I say this, even though I'm vested in another high-performance language, Julia, for which I've written extensively (my books on Julia) and continue to use up to this day. However, unlike those fanboys of this or the other data science language, I'm open to new possibilities, which I'm always eager to explore. So, even though I'm a long way from being a Rust veteran, I can see its merit in our field.

So far, there are a few Rust packages for ML work, such as Smartcore and Linfa (plant juice in Italian), though, in all fairness, this codebase is nowhere near the variety and maturity of the likes of Scikit-learn in Python and the packages in the Julia ecosystem. Still, there is a lot of value Rust offers in this space, and as the community grows, we should be expecting to see the ML and A.I. libraries of Rust grow both in number and sophistication.

Final thoughts
It may seem a bit too early to tell, but it's not far-fetched to say that Rust is here to stay and make it.  While high-level languages like Python had nothing more to offer than simplicity and ease-of-use (probably the main reason they made it to the data science world), Rust is closer to modern languages like Julia and Nim, which offer a serious performance boost. Its business proposition is unquestionable, its adoption higher than many people expected, and its potential of making a dent in machine learning is hard to contest. Once you get past its eccentric programming style, you may begin to view it with the respect and fondness it deserves. So, check it out when you have a moment. Cheers!