Clustering Is a Hard Problem That Has to Be Tackled in a Stochastic Manner, Right?

Short answer: Nope! Longer answer: clustering can be a simple deterministic problem, given that you figure out the optimal centroids to start with. But isn’t the latter the solution of a stochastic process though? Again, nope. You can meander around the feature space like a gambler, hoping to find some points that can yield a good solution, or you can tackle the whole problem scientifically. To do that, however, you have to forget everything you know about clustering and even basic statistics, since the latter are inherently limited and frankly, somewhat irrelevant to proper clustering.

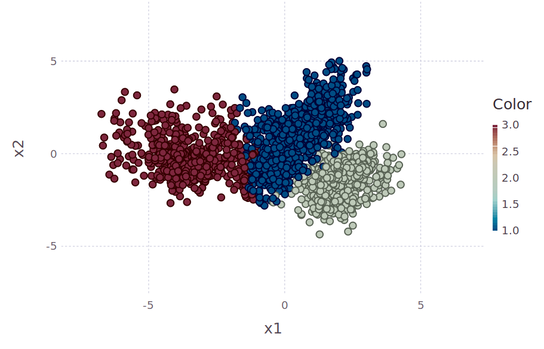
Finding the optimal clusters is a two-fold problem: 1. you need to figure out which solutions make sense for the data (i.e. a good value for K), and 2. figure out these solutions in a methodical and robust manner. The former has been resolved as a problem and it’s fairly trivial. Vincent Granville talked about it in his blog, many years ago and since he is better at explaining things than I am, I’m not going to bother with that part at all. My solution to it is a bit different but it’s still heuristics-based. The 2nd part of the problem is also the more challenging one since it’s been something many people have been pursuing a while now, without much success (unless you count the super slow method of DBSCAN, with more parameters than letters in its name, as a viable solution).

To find the optimal centroids, you need to take into account two things, the density of each centroid and the distances of each centroid to the other ones. Then you need to combine the two in a single metric, with you need to maximize. Each one of these problems seems fairly trivial, but something that many people don’t realize is that in practice, it’s very very hard, especially if you have multi-dimensional data (where conventional distance metrics fail) and lots of it (making the density calculations a major pain). Fortunately, I found a solution to both of these problems using 1. a new kind of distance metric, that yields a higher U value (this is the heuristic used to evaluate distance metrics in higher dimensional space), though with an inevitable compromise, and 2. a far more efficient way of calculating densities. The aforementioned compromise is that this metric cannot guarantee that the triangular inequality holds, but then again, this is not something you need for clustering anyway. As long as the clustering algo converges, you are fine.

Preliminary results of this new clustering method show that it’s fairly quick (even though it searches through various values of K to find the optimum one) and computationally light. What’s more, it is designed to be fairly scalable, something that I’ll be experimenting with in the weeks to come. The reason for the scalability is that it doesn’t calculate the density of each data point, but of certain regions of the dataset only. Finding these regions is the hardest part, but you only need to do that once, before you start playing around with K values.

Anyway, I’d love to go into detail about the method but the math I use is different to anything you’ve seen and beyond what is considered canon. Then again, some problems need new math to be solved and perhaps clustering is one of them. Whatever the case, this is just one of the numerous applications of this new framework of data analysis, which I call AAF (alternative analytics framework), a project I’ve been working on for more than 10 years now. More on that in the coming months.