Overview of Dimensionality Reduction Methods

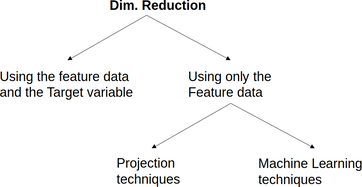
Dimensionality reduction is the methodology involving the coding of a dataset's information into a new one consisting of a smaller number of features. This approach tries to address the curse of dimensionality, which involves the difficulty of handling data that comprises too many variables. This article will explore a primary taxonomy of dimensionality reduction and how this methodology ties into other aspects of data science work, particularly machine learning.

There are several types of dimensionality reduction out there. You can split them into two general categories: methods involving the feature data in combination with the target variable, and methods involving the feature data only. Additionally, the second category methods can be split into those involving projection techniques (e.g., PCA, ICA, LDA, Factor Analysis, etc.), and those based on machine learning algorithms (e.g., Isomap, Self-organizing maps, Autoencoders, etc.). You can see a diagram of this classification below.

The most noteworthy dimensionality reduction methods used today are Principle Components Analysis (PCA), Uniform Manifold Approximation and Projection (UMAP), and Autoencoders. However, in cases where the target variable is used, feature selection is a great alternative. Note that you can always combine different dimensionality reduction methods for even better results. This strategy works particularly well when the methods come from different families.

It's important to remember that dimensionality reduction is not always required, no matter how powerful it is as a methodology. Sometimes the original features are good enough, while the project requires a transparent model, something not always feasible when dimensionality reduction is involved. What's more, dimensionality reduction always involves some loss of information, so sometimes it's not a good idea. It's crucial to gauge all the pros and cons of applying such an approach before doing so, since it may sometimes not be worth it because of the compromises you have to make.

Many of the datasets found in data science projects today involve variables that are somehow related to each other, though this correlation is a non-linear one. That's why many traditional dimensionality reduction methods may not be as good, especially if the datasets are complex. That's why machine learning methods are more prevalent in cases like this and why there is a lot of research in this area. What's more, these dimensionality reduction methods integrate well with other machine learning techniques (e.g., in the case of autoencoders). This fact makes them a useful addition to a data science pipeline.

In my book Julia for Machine Learning, I dedicate a whole chapter in dimensionality reduction, focusing on these relatively advanced methods. Additionally, I cover other machine learning techniques, including several predictive models, heuristics, etc. So, if you want to learn more about this subject, check it out when you have the chance. Cheers!