The Numgame Puzzle and a Heuristic to Solve It

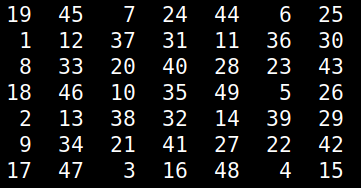
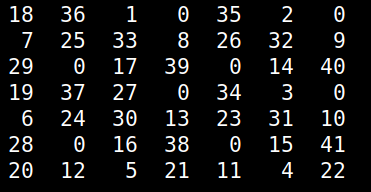
For over 2 decades there is a puzzle game I've played from time to time, usually to pass the time creatively or to challenge myself in algorithm development. This game, which I was taught by a friend, didn't have a name and I never managed to find it elsewhere so I call it Numgame (as it involves numbers and it's a game). Over the years, I managed to solve many of its levels though I never got an algorithm for it, until now.

The game involves a square grid, originally a 10-by-10 one. The simplest grid that's solvable is the 5-by-5 one. The object of the game is to fill the grid with numbers, starting from 1 and going all the way to n^2, where n is the size of the grid, which can be any number larger than 4 (grids of this size or lower are not solvable).

To fill the grid, you can "move" horizontally, vertically and diagonally, as long as the cell you go to is empty. When moving horizontally or vertically you need to skip 2 squares, while when you move diagonally you need to skip 1. Naturally, as you progress, getting to the remaining empty squares becomes increasingly hard. That's why you need to have a strategy if you are to finish the game successfully.

Naturally, not all starting positions yield a successful result. Although more often than not you'd start from a corner, you may choose to start from any other square in the grid. That's useful, considering that some grids are just not solvable if you start from a corner (see image below; empty cells are marked as zeros)

Before we look at the solution I've come across, try to solve a grid on your own and think about a potential algorithm to solve any grid. At the very least, you'll gain an appreciation of the solution afterward.

Anyway, the key to solving the Numgame levels is to use a heuristic that will help you assess each move. In other words, you'll need to figure out a score that discerns between good and bad positions. The latter result from the various moves. So, for each cell in the grid, you can count how many legitimate ways are there for accessing it (i.e. ways complying with the aforementioned rules). You can store these numbers in a matrix. Then, you can filter out the cells that have been occupied already, since we won't be revisiting them anyway. This leaves us with a list of numbers corresponding to the number of ways to reach the remaining empty cells.

Then we can take the harmonic mean of these numbers. I chose the harmonic mean because it is very sensitive to small numbers, something we want to avoid. So, the heuristic will take very low values if even a few cells start becoming inaccessible. Also, if even a single cell becomes completely inaccessible, the heuristic will take the value 0, which is also the worst possible score. Naturally, we aim to maximize this heuristic as we examine the various positions stemming from all the legitimate moves of each position. By repeating this process, we either end up with a full grid or one that doesn't progress because it's unsolvable.

This simple problem may seem obvious now, but it is a good example of how a simple heuristic can solve a problem that's otherwise tough (at least for someone who hasn't tackled it enough to figure out a viable strategy). Naturally, we could brute-force the whole thing, but it's doubtful that this approach would be scalable. After all, in the era of A.I. we are better off seeking intelligent solutions to problems, rather than just through computing resources at them!